4.2 이산분포
4.2.1 베르누이 분포와 이항분포
import numpy as np
from scipy import stats as st
from matplotlib import pyplot as plt
st.binom.pmf(n=10,p=0.3,k=[0,1,2,3,4,5])
# 예제 4.2.1 (b)
# x값이 (1,3,6)일 경우 각 값까지의 누적확률 구하기
np.round(st.binom.cdf(n=10,p=0.3,k=[1,3,6]),3)
# 예제 4.2.1 (c)
# 0.2, 0.5, 0.8의 누적확률을 갖는 확률변수값 구하기
st.binom.ppf(n=10,p=0.3,q=[0.2,0.5,0.8])
# 예제 4.2.1 (d)
# 이항분포 B(10, 0.3)를 따르는 난수 5개 얻기
st.binom.rvs(n=10,p=0.3,size=5)
4.2.2 포아송 분포
# 예제 4.2.2 (a)
# 0,1,2,3,4,5 값에 대한 확률값 구하기
st.poisson.pmf(mu=3,k=[0,1,2,3,4,5])
# 평균 3인 포아송분포를 따르는 경우 P(X<=3) 구하기
st.poisson.cdf(mu=3,k=3)
# 평균 3인 포아송분포를 따르는 경우 P(X>=4) 구하기
1-st.poisson.cdf(mu=3,k=3)
# 평균 3인 포아송분포를 따르는 경우 P(3<=X<=5) 구하기
# P(3<=X<=5) = P(X<=5) - P(X<=2)
st.poisson.cdf(mu=3,k=5)-st.poisson.cdf(mu=3,k=2)
# 평균 3인 포아송분포를 따르는경우 P(X>5)
1-st.poisson.cdf(mu=3,k=5)# 예제 4.2.2 (i)
# 평균 3인 포아송 분포의 확률질량함수 구하기
bins=np.arange(0,10,1)
y1=st.poisson.pmf(mu=3,k=bins)
plt.bar(bins,y1,color='red',alpha=0.3)
plt.xlabel('x')
plt.ylabel('$p(x)$')
plt.show()
4.3 정규성 검정
# 예제 4.3.1
# 표준정규분포에서 난수 발생으로 표본에 대해 히스토그램 그리기
import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import probplot
import seaborn as sns
n=50
x1=np.random.normal(0,1,n)
x2=np.random.normal(0,1,n)
x3=np.random.normal(0,1,n)
x4=np.random.normal(0,1,n)
x5=np.random.normal(0,1,n)
plt.figure(figsize=(12,8))
plt.subplot(2,3,1)
plt.hist(x1, density=True, color='r')
plt.title('Normal(0,1)')
plt.subplot(2,3,2)
sns.distplot(x2)
plt.title('Normal(0,1)')
plt.subplot(2,3,3)
sns.distplot(x3, hist=True, kde=True,
kde_kws={'shade':True, 'linewidth':3})
plt.subplot(2,3,4)
plt.hist(x4)
plt.subplot(2,3,5)
plt.hist(x5, histtype='bar', rwidth=0.8)
# 예제 4.3.2 (a)
# 표준정규분포에서 발생한 랜덤 데이터에 대해 Q-Q그림
import numpy as np
import statsmodels.api as sm
import pylab as py
data_n=np.random.normal(0,1,100)
sm.qqplot(data_n,line='45')
py.show()
'표준정규분포의 QQ그림'
샤피로-윌크 검정(Sapiro-Wilk test) : 데이터의 정규성 검정방법
- 귀무가설(H0): 데이터는 정규분포를 따른다.
- 대립가설(H1): 데이터는 정규분포를 따르지 않는다.
from scipy import stats as st
x=st.norm.rvs(0,1,size=10)
st.shapiro(x)
# 기각하지 못하므로 정규분포를 따름
p-value가 0.69로 유의수준 0.05보다 크므로 귀무가설 기각하지 못함
즉, 정규분포를 따른다!
# 예제 4.3.2 (c)
# 여러 분포에서 발생한 랜덤 표본에 대해 정규성 검토
from scipy.stats import probplot
np.random.seed(0)
n=100
x1=np.random.normal(0,1,n)
x2=np.random.exponential(2,n)
x3=np.random.uniform(0,1,n)
f,axes=plt.subplots(2,3,figsize=(12,6))
axes[0][0].boxplot(x1)
probplot(x1,plot=axes[1][0])
axes[0][1].boxplot(x2)
probplot(x2,plot=axes[1][1])
axes[0][2].boxplot(x3)
probplot(x3,plot=axes[1][2])
plt.show()# 4장 연습문제 12번
from scipy.stats import probplot
np.random.seed(0)
n=100
x1=np.random.normal(0,1,n)
x2=np.random.exponential(2,n)
x3=np.log(x2)
f,axes=plt.subplots(2,3,figsize=(12,6))
axes[0][0].boxplot(x1)
probplot(x1,plot=axes[1][0])
axes[0][1].boxplot(x2)
probplot(x2,plot=axes[1][1])
axes[0][2].boxplot(x3)
probplot(x3,plot=axes[1][2])
plt.show()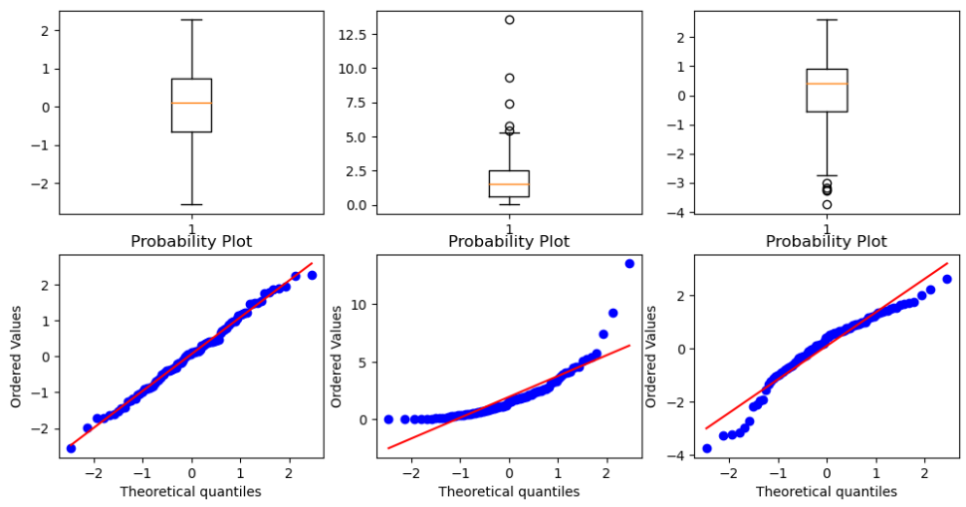
4.4 모의실험
중심극한정리(Central Limit Theorem, CLT) :
주어진 모집단이 어떠한 분포를 가지고 있더라도, 그 모집단에서 크기가 큰 표본을 여러 번 추출할 때, 이 표본들의 평균은 정규분포를 따르게 된다. 특히, 표본의 크기가 충분히 크고 모집단의 분포가 어떤 모양이든 상관없이, 표본 평균들의 분포는 정규분포에 수렴하게 된다.
# 4.4.2 중심극한정리와 모의실험
# 4.4.2(a)
# 균일분포의 확률밀도함수선 그리기
import seaborn as sns
def sampling2pdf(n,m=100):
mean_of_samples =[]
for i in range(m):
samples=st.uniform.rvs(loc=0,scale=1,size=n)
mean_of_samples.append(np.mean(samples))
return mean_of_samples
samples1=sampling2pdf(5)
samples2=sampling2pdf(10)
samples3=sampling2pdf(20)
samples4=sampling2pdf(30)
sns.kdeplot(samples1,color='green',label='n=5',linestyle='--')
sns.kdeplot(samples2,color='grey',label='n=10',linestyle='-.')
sns.kdeplot(samples3,color='blue',label='n=20',linestyle='dashed')
sns.kdeplot(samples4,color='red',label='n=30',linestyle='solid',linewidth=3.0)
plt.legend(title='sample size')
# 4.4.2 (b)
# 지수분포의 확률밀도함수선 그리기
import seaborn as sns
def sampling2pdf(n,m=100):
mean_of_samples =[]
for i in range(m):
samples=st.expon.rvs(loc=0,scale=1,size=n)
mean_of_samples.append(np.mean(samples))
return mean_of_samples
samples1=sampling2pdf(5)
samples2=sampling2pdf(10)
samples3=sampling2pdf(20)
samples4=sampling2pdf(30)
sns.kdeplot(samples1,color='green',label='n=5',linestyle='--')
sns.kdeplot(samples2,color='grey',label='n=10',linestyle='-.')
sns.kdeplot(samples3,color='blue',label='n=20',linestyle='dashed')
sns.kdeplot(samples4,color='red',label='n=30',linestyle='solid',linewidth=3.0)
plt.legend(title='sample size')
5장. 일변량 데이터와 기술통계량
# 5.1.3(b)
plt.rcParams['figure.figsize']=[12,8]
store=('A','B','C','D','E')
sales=[3,12,5,25,45]
y_pos=np.arange(len(store))
# startangel : 첫 번째 pie 시작 각도
cols=['gold','yellowgreen','lightcoral','lightskyblue','red']
explode=(0.0, 0.1, 0.0, 0.0, 0.0) #확대
plt.subplot(1,3,1)
plt.pie(sales,labels=store)
plt.subplot(1,3,2)
plt.pie(sales,labels=store,explode=explode)
plt.subplot(1,3,3)
plt.pie(sales,labels=store,explode=explode,
autopct='%1.1f%%', shadow=True, startangle=90, colors=cols)
plt.title('Store sales')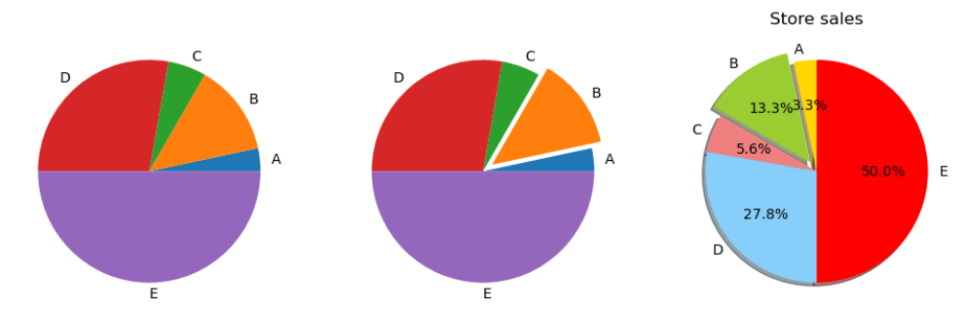
# 예제 5.2.1 농구시합 데이터에 대해 줄기-잎 그림 그리기
import sys
!{sys.executable} -m pip install stemgraphic
import stemgraphic
x=np.array([45,86,34,98,67,78,56,45,85,75,64,75,
75,75,58,45,83,74])
stemgraphic.stem_graphic(x, scale=10)
# 예제 5.2.7 (a)
y=st.norm.rvs(loc=0,scale=1,size=10)
n=len(y)
m=np.mean(y)
sd=np.std(y,ddof=1)
cri=st.t.ppf(df=n-1,q=0.975) # 95%이지만 q= 0.975이므로 주의!!!'파이썬 > 통계전산처리' 카테고리의 다른 글
| 통계전산처리 - 9주차(연속분포) (0) | 2024.09.05 |
|---|---|
| 통계전산처리 - 7주차 (다양한 시각화) (0) | 2024.09.05 |
| 통계전산처리 - 6주차 (데이터프레임 다루기, 그래프 그리기) (1) | 2024.09.03 |
| 통계전산처리 - 2장 연습문제 풀이 (0) | 2024.09.03 |
| 통계전산처리 - 5주차 (행렬연산, 반복문) (1) | 2024.09.03 |