
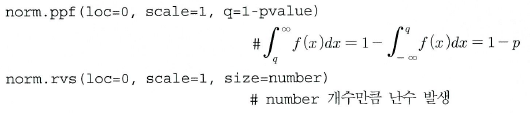
import numpy as np
from scipy import stats as st
from matplotlib import pyplot as plt
mu=0
sigma=1
x=np.linspace(mu-4*sigma,mu+4*sigma,100) # 표준정규분포 x값의 범위 -4 ~ +4
y=st.norm.pdf(x,mu,sigma) # 정규분포에 의한 확률밀도함수의 값
xx=np.linspace(mu-4*sigma,mu-1*sigma,100) # P(Z<-1)
yy=st.norm.pdf(xx,mu,sigma)
plt.plot(x,y,'red')
plt.title('$Probability$ $Density$ $Function$')
plt.xlabel('x')
plt.ylabel('$p(x)$')
plt.fill_between(xx,yy,alpha=0.5)
plt.text(-1.5,0.07,'$P(Z<-1)$',fontsize=13,color='black')
plt.show()
mu=0
sigma=1
x=np.linspace(mu-4*sigma,mu+4*sigma,100) # 표준정규분포 x값의 범위 -4 ~ +4
y=st.norm.pdf(x,mu,sigma) # 정규분포에 의한 확률밀도함수의 값
xx=np.linspace(mu-1*sigma,mu+4*sigma,100) # P(Z > -1)
yy=st.norm.pdf(xx,mu,sigma)
plt.plot(x,y,'red')
plt.title('$Probability$ $Density$ $Function$')
plt.xlabel('x')
plt.ylabel('$p(x)$')
plt.fill_between(xx,yy,alpha=0.5)
plt.text(-0.7,0.15,'$P(Z>-1)$',fontsize=13,color='black')
plt.show()
x=np.arange(-3,3,step=0.1)
plt.plot(x,st.norm.pdf(x=x),color='black',linestyle='dotted')
plt.plot(x,st.t.pdf(x=x,df=5), color='green')
# 예제 4.1.5 (g)
# 분자자유도 3, 분모자유도 10인 F 분포의 확률밀도함수 그리기
grid=np.linspace(0,10,100)
y1=st.f.pdf(dfn=3,dfd=10,x=grid)
y2=st.f.pdf(dfn=8,dfd=10,x=grid)
plt.figure(figsize=(10,5))
plt.plot(grid,y1,'red',label='numerator df=3, den df=10')
plt.plot(grid,y2,'blue',label='numerator df=5, den df=10')
plt.title('$Probability$ $Density$ $Functions$')
plt.xlabel('x')
plt.ylabel('$p(x)$')
plt.ylim(0,1.2)
plt.legend()
plt.show()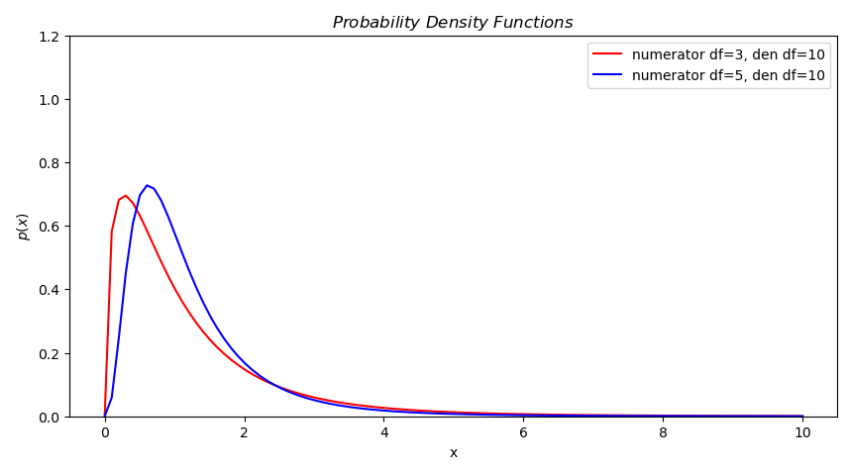
# 예제 4.1.6 (i)
# 자유도 5인 t 분포, 표준정규분포, 평균 1인 지수분포, [0,2]에서의 균일 분포에 대한 확률밀도함수 그리기
x=np.arange(-4,4,step=0.1)
plt.subplot(2,2,1)
plt.plot(x,st.norm.pdf(x=x),color='black',linestyle='dotted')
plt.title('Normal(0,1)')
plt.subplot(2,2,2)
plt.plot(x,st.t.pdf(x=x,df=5),color='green')
plt.title('t with df = 5')
plt.subplot(2,2,3)
plt.plot(x,st.expon.pdf(scale=1,x=x), color='m', linestyle='dashed')
plt.xlabel('Exponential with mean =1')
plt.subplot(2,2,4)
plt.plot(x,st.uniform.pdf(loc=0,scale=2,x=x),color='red',linestyle='-')
plt.xlabel('Uniform [0,2]')
# 4장 연습문제 7번
# (a)
st.t.sf(df=10,x=2.5)
# (b)
st.t.cdf(df=10,x=-2.5)
# (c)
st.t.sf(df=10,x=1.8)+st.t.cdf(df=10,x=-1.8)
# (d)
st.t.sf(df=10,x=2.5)
# (e)
st.t.cdf(df=10,x=-2.5)
# (f)
st.t.cdf(df=10,x=1.5)-st.t.cdf(df=10,x=-1)

# 4장 연습문제 3번
# (a)
st.norm.ppf(loc=10,scale=3,q=0.6)
# (b)
st.norm.sf(loc=10,scale=3,x=12)
# (c)
st.norm.sf(loc=10,scale=3,x=-11.5)-st.norm.sf(loc=10,scale=3,x=11.5)'파이썬 > 통계전산처리' 카테고리의 다른 글
| 통계전산처리 - 10주차(이산분포, 정규성검정, 모의실험) (3) | 2024.09.05 |
|---|---|
| 통계전산처리 - 7주차 (다양한 시각화) (0) | 2024.09.05 |
| 통계전산처리 - 6주차 (데이터프레임 다루기, 그래프 그리기) (1) | 2024.09.03 |
| 통계전산처리 - 2장 연습문제 풀이 (0) | 2024.09.03 |
| 통계전산처리 - 5주차 (행렬연산, 반복문) (1) | 2024.09.03 |